La propagation des ondes radioélectriques à l'intérieur et à l'extérieur des bâtiments
Tables de matières
|
1 - Introduction * 2 – Les ondes électromagnétiques * 3 – Les différents mécanismes de propagation * 3.1 – Les trajets directs * 3.2 – Les trajets transmis * 3.3 – Les trajets réfléchis * 3.3.1 - La réflexion spéculaire *3.3.2 - La réflexion diffuse *3.3.2.1 - Le modèle de LAMBERT *3.3.2.2 - Le modèle de PHONG *3.4 – Les trajets diffractés * 3.5 – Les trajets guidés * 4 – Les propriétés du canal * 4.1 – Affaiblissement * 4.2 – Variabilité * 4.3 – Sélectivité * 4.3.1 – Densité de puissance moyenne *4.3.2 – Le retard moyen *4.3.3 – La dispersion des retards *4.3.4 – L'intervalle des retards *4.3.5 – La fenêtre des retards *4.3.6 – La bande de cohérence * |
5 – Les différents modèles de propagation * 5.1 - Les modèles macro cellulaires * 5.1.1 - Les modèles ruraux *5.1.2 - Le modèle montagneux *5.2 - Les modèles petites cellules * 5.3 - Les modèles micro cellulaires * 5.3.1 - Calcul le long des rues *5.3.2 - Calcul sur le profil *5.4 – Modèle à lancer de rayons * 5.5 - Modèle de pénétration * 5.6 – Modèles à l'intérieur des bâtiments * 5.6.1 – Modèles empiriques *5.6.2 – Modèles déterministes *5.7 – Les modèles à rayons * Figure 12 : exemple de tracé à l'extérieur des bâtiments * 6 – Conclusion * 7 – Bibliographie * |
La communication sans fils entre objets requiert une bonne connaissance du canal de propagation radioélectrique. Il est en effet nécessaire d'évaluer au préalable le comportement des ondes dans l'environnement considéré pour pouvoir ensuite paramétrer la puissance d'émission, la polarisation, … et choisir les antennes, la modulation, le protocole de transmission, …
Une première partie de l'exposé consistera à définir succinctement ce qu'est une onde radioélectrique puis présentera les différents phénomènes pouvant l'affecter (réflexion, transmission, diffraction, diffusion).
Dans une deuxième partie seront détaillées les difficultés de transmission résultant des interactions des ondes, entre elles et avec l'environnement, qu'il soit "indoor" ou "outdoor" (masquage, brouillage, fading, …).
Une dernière partie abordera les techniques disponibles pour l'étude de la propagation entre objets communicants, une large part étant faite aux modèles de propagation dans différents environnements (rural, montagneux, suburbain, urbain, intérieur des bâtiments, …, etc.) : macro cellulaire, petite cellule, micro cellulaire, intérieur des bâtiments, modèle à lancer et à tracé de rayon. Ces deux derniers sont plus particulièrement adaptés à la compréhension et à l'illustration des différents phénomènes, à l'intérieur comme à l'extérieur des bâtiments.
2 – Les ondes électromagnétiques
Les paramètres permettant de caractériser la propagation des ondes électromagnétiques sont le champ électrique![]() , le champ magnétique
, le champ magnétique![]() , l'induction électrique
, l'induction électrique![]() et l'induction magnétique
et l'induction magnétique![]() . Seuls les vecteurs
. Seuls les vecteurs ![]() et
et ![]() produisent des actions par lesquelles il est possible de mesurer le champ électromagnétique. Les vecteurs
produisent des actions par lesquelles il est possible de mesurer le champ électromagnétique. Les vecteurs ![]() et
et ![]() sont reliés aux vecteurs
sont reliés aux vecteurs ![]() et
et ![]() par les relations linéaires suivantes :
par les relations linéaires suivantes :
![]() et
et ![]()
Les coefficients ε et μ sont respectivement la permittivitι et la permι
abilité magnétique du milieu.En l'absence de particules chargées, ils sont reliés entre eux par les équations de Maxwell :
rot ![]() =
= ![]() +
+ ![]()
![]() /
/ ![]() t
t
rot ![]() = -
= - ![]()
![]() /
/ ![]() t
t
div ![]() = 0
= 0
div ![]() = 0
= 0
Leur résolution nous amène à l'équation de HELMOLTZ pour chacun des vecteurs ![]() ,
, ![]() ,
,![]() et
et ![]() . Pour le vecteur
. Pour le vecteur ![]() (où
(où ![]() appartient à l'ensemble
appartient à l'ensemble![]() ,
, ![]() ,
, ![]() ou
ou ![]() ) nous avons :
) nous avons :
(D - e m ![]() 2/
2/![]() t2)
t2) ![]() = 0
= 0
où :
D
est l'opérateur laplacien : grad(div) - rot (rot)En régime sinusoïdal les oscillations des vecteurs E et H se propagent dans l'espace perpendiculairement l'un par rapport à l'autre sous la forme d'une onde (cf. figure 1) à la vitesse ![]() . La longueur d'onde, distance pour laquelle la phase de l'onde varie de 2π, est donnιe par la relation :
. La longueur d'onde, distance pour laquelle la phase de l'onde varie de 2π, est donnιe par la relation :
![]()
où :
f est la fréquence de l'onde,
ω est la pulsation
T est la période
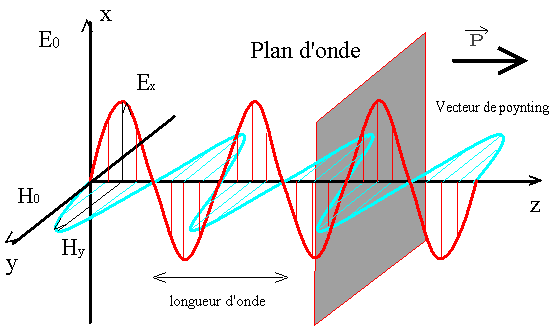
Figure 1 : Illustration de la propagation d'une onde électromagnétique
Le vecteur de Pointing décrit l'amplitude et la direction du flux de puissance transportée.
Les équations de Maxwell sont généralement très difficiles à mettre en œuvre pour analyser les problèmes posés et on a souvent recours à des méthodes approchées. La taille de l'irrégularité d rencontrée au cours de la propagation par rapport à la longueur d'onde (relié à la fréquence) joue un rôle important. On considère les trois cas suivants :
- ![]() : l'irrégularité est très petite par rapport à la longueur d'onde; on applique les méthodes statistiques.
: l'irrégularité est très petite par rapport à la longueur d'onde; on applique les méthodes statistiques.
- ![]() : l'irrégularité est de la taille de la longueur d'onde; les approximations ne sont pas possibles (zone de résonance).
: l'irrégularité est de la taille de la longueur d'onde; les approximations ne sont pas possibles (zone de résonance).
3 – Les différents mécanismes de propagation
Les trajets de propagation (cf. figure 2) sont de différente nature : directs, transmis, réfléchis ou diffusés, diffractés ou guidés.

Figure 2 : Les différents mécanismes de propagation
Un trajet est dit direct lorsque l'émetteur et le récepteur sont en visibilité radioélectrique : le premier ellipsoïde de Fresnel n'est pas obstrué. Ce dernier délimite la région de l'espace où passe la quasi-totalité de l'énergie. Il est le lieu des points M qui vérifie l'équation suivante (E désigne l'emplacement de l'émetteur, R celui du récepteur) :
![]()
La plupart du temps le trajet direct n'existe pas : il est obstrué par des obstacles (masques). La transmission est le phénomène qui permet aux ondes de traverser un obstacle (mur, immeuble, végétation, …etc.).
La réflexion se produit lorsque l'onde rencontre une surface dont les dimensions sont grandes par rapport à la longueur d'onde (sol, mur, façade d'immeuble, …., etc.).
Les caractéristiques de réflexion d'une surface quelconque dépendent de plusieurs facteurs : la surface du matériau (lisse ou rugueux), de la longueur d'onde du rayonnement incident et de l'angle d'incidence.
La rugosité de la surface relativement à la longueur d'onde constitue un paramètre important de la forme du diagramme de réflexion. Une surface lisse réfléchi le rayonnement incident dans une seule direction telle un miroir (on parlera de réflexion spéculaire). Une surface rugueuse, au contraire réfléchira le rayonnement incident dans toutes les directions.
Une surface est considérée comme rugueuse, selon le critère de Rayleigh, si la relation suivante est satisfaite :
![]()
où :
Pour un rayonnement infrarouge caractérisé par une longueur d'onde de 1550 nm, sous incidence normale, une surface est dite rugueuse si la hauteur maximale des irrégularités ς est supérieure à 0,19 μm. Ce rιsultat montre que la plupart des surfaces rencontrιes à l'intérieur des bâtiments sont considérées comme rugueuses au rayonnement infrarouge, le diagramme de réflexion présente une composante diffuse (on parlera de réflexion diffuse).
3.3.1 - La réflexion spéculaire
La réflexion spéculaire, phénomène commun à toutes fréquences, est celle due à une surface homogène parfaitement plane. L'affaiblissement de propagation induit par de telles réflexions découle des relations de Fresnel et dépend des caractéristiques diélectriques de la surface réfléchissante (conductivité σ, permittivité ε). A titre d'exemple, la plupart des surfaces indoor ont un coefficient re réflexion en infra rouge compris entre 0.4 et 0.9 [GFELLER, 1979]. Différents coefficients de réflexion ont été mentionnés dans la littérature pour différents matériaux [YANG, 2000].
La réflexion diffuse est due aux réflexions par des surfaces qui ne sont pas planes mais rugueuses; les surfaces présentent des irrégularités. Il en résulte qu'une onde incidente n'est plus réfléchie dans une direction unique mais diffusée dans de multiples directions. Deux modèles sont couramment utilisés pour représenter la réflexion du rayonnement infra rouge : le modèle de Lambert et le modèle de PHONG.
3.3.2.1 - Le modèle de LAMBERT
Certaines surfaces sont très irrégulières et réfléchissent le rayonnement infra rouge par exemple dans toutes les directions indépendamment du rayonnement incident. De telles surfaces sont dites diffuses et peuvent être représentées par le modèle de LAMBERT. Le modèle est très simple et très facile d'implantation dans les logiciels de calcul. Il est décrit par l'équation suivante :
![]()
où :
est l'angle d'observation.
Le diagramme de réflexion de plusieurs surfaces rugueuses est bien représenté par le modèle de LAMBERT excepté autour de la réflexion spéculaire ou le diagramme présente une composante importante. Le modèle de PHONG considère le diagramme de réflexion comme la somme de deux composantes : la composante diffuse et la composante spéculaire. Le pourcentage de chaque composante dépend principalement des caractéristiques de la surface et est un paramètre du modèle. La composante diffuse est modélisé par le modèle de LAMBERT. La composante spéculaire est modélisée par une fonction qui dépend de l'angle d'incidence ![]() et de l'angle d'observation (angle de réflexion)
et de l'angle d'observation (angle de réflexion) ![]() . Le modèle de PHONG est décrit par le modèle ci-dessous :
. Le modèle de PHONG est décrit par le modèle ci-dessous :
![]()
où :
est l'angle d'observation.
On notera que le modèle de LAMBERT est obtenu à partir de celui de PHONG en prenant rd égale à zéro. Le modèle de PHONG, dépendant de l'angle d'observation et de l'angle d'incidence, est plus complexe que le modèle de LAMBERT. Les temps de calculs s'en trouvent allongés. Le diagramme de réflexion présente un module principal centré autour de la direction de la réflexion spéculaire.
La diffraction se produit lorsqu'une onde rencontre une arête (colline, immeuble, végétation, toits, coins de bâtiments, structures routières, …, etc.) dont les dimensions sont grandes devant la longueur d'onde. Elle constitue l'un des facteurs les plus importants intervenant dans la propagation des ondes radioélectriques [BOITHIAS, 1983]. L'utilisation de la Théorie Géométrique de la Diffraction (TGD) permet de représenter ce phénomène sous forme de rayons [McNAMARA, 1990]. Des expressions approchées ont été proposées quant à l'évaluation de l'affaiblissement par diffraction [BOITHIAS, 1983]:
![]() pour >-0.7 et utilisable au voisinage de 0.
pour >-0.7 et utilisable au voisinage de 0.
![]() valable pour >1,5
valable pour >1,5
où :
- 
- d1 et d2 sont respectivement les distances de l'arête à l'émetteur et au récepteur.
Le lecteur trouvera ci-après, à titre d'exemple quelques valeurs typiques d'affaiblissement à 4 fréquences (20, 40, 60 et 100 GHz) pour des arêtes (de hauteur 1 et 10 m) situées à 1 km de l'émetteur et du récepteur.
Les résultats sont résumés dans le tableau ci-dessous :
|
Affaiblissement de diffraction |
d=1 km, h=1m |
d=1km, h=10m |
|
Fréquence=20 GHz |
10 |
30.3 |
|
Fréquence =40 GHz |
14 |
33.3 |
|
Fréquence=60 GHz |
16 |
35 |
|
Fréquence=100 GHz |
18 |
37 |
Tableau 1 : Valeurs typiques d'affaiblissement par diffraction
Certains environnements (rues encaissées, corridors, tunnels, etc.) se comportent comme de véritables guides d’ondes vis-à-vis de la propagation des ondes radioélectriques consécutivement à de multiples réflexions successives sur les parois (application de la théorie des modes de propagation et celle des rayons plus particulièrement lorsque la longueur d’onde est très petite par rapport à la section transverse du tunnel par exemple).
Ces différents trajets, d'amplitude et de phase différentes interfèrent en arrivant au récepteur. Les interférences sont soit constructives (les trajets arrivent en phase) d'où renforcement du signal, soit destructive, on a alors un évanouissement du signal. De plus il est à noter que le mobile se déplace dans cette figure d'interférences. Il voit successivement des tâches lumineuses et des tâches sombres (les franges d'interférences) provoquant des évanouissements du signal.
Du fait de la présence de trajets multiples et du déplacement de la station de réception, le canal de propagation possède trois propriétés fondamentales : affaiblissement, variabilité et sélectivité en fréquence.
En analogique, la notion d'affaiblissement était suffisante pour étudier le canal de propagation. En contexte de communication numérique, les évanouissements dus à la variabilité et à la sélectivité induisent des dégradations de la qualité de la communication indépendamment de l'affaiblissement.
On distingue généralement l'affaiblissement de propagation en espace libre et l'affaiblissent en excès par rapport à ce dernier.
L'affaiblissement en espace libre l'affaiblissement de transmission est du à la dispersion de l'énergie au fur et à mesure que l'on s'éloigne de l'émetteur. Il est donné par la relation suivante :
![]()
où :
d est la distance entre l'émetteur et le récepteur,
l est la longueur d'onde,
f est la fréquence.
Exemple :
d = 1 km
f = 900 MHz, A0 = 91.4 dB
f = 1800 MHz, A0 = 97.4 dB
Ceci suppose que l'on a qu'un seul trajet radioélectrique dont le 1er ellipsoïde de FRESNEL est dégagé. C'est une expression en 1/d2 (conservation de l'énergie). Cela veut dire que l'on perd 6 dB chaque fois quel l'on double la distance.
L'affaiblissement en excès par rapport à l'espace libre est la différence entre l'affaiblissement de propagation et l'affaiblissement en espace libre (absorption par les gaz, les hydrométéores, les murs, la végétation, affaiblissement par diffraction, …, etc..
L’environnement de propagation est fluctuant : le passage de véhicules et de personnes, le vent dans les arbres, l’ouverture de portes provoquent des fluctuations des trajets radioélectriques et génèrent les variations rapides du signal observé. Combinés avec le mouvement des véhicules, ces phénomènes créent une variabilité du canal de propagation dans l’espace et dans le temps.
Les variations du signal sont de nature aléatoire. Une analyse statistique permettra d’évaluer l’impact des trajets multiples sur la transmission des systèmes radio-mobiles. La loi du champ reçu et le temps moyen des évanouissements par exemple sont des données indispensables pour dimensionner les équipements de transmission et leur dispositif de lutte contre le fading (entrelacement, diversité).
Une modélisation des variations rapides a été proposée [CLARKE, 1968]. En supposant que le mobile se déplace dans une figure d’interférence générée par la superposition d’un grand nombre d’ondes planes d’amplitudes, de phases et de directions aléatoires indépendantes, le champ reçu (l’enveloppe complexe) est, par l’application du théorème de la limite centrale, une variable gaussienne. L’enveloppe du signal à bande étroite, la puissance reçue, suit alors une loi de Rayleigh. On parlera de fading de Rayleigh.
Dans le cas d’un trajet prédominant (visibilité, environnement ouverts tels que banlieue, rural, etc.), l’enveloppe du signal à bande étroite, la puissance reçue, suit alors une loi de Rice. Il est observé lorsqu’un des trajets est prédominant. La loi de Rice correspond à une loi de Rayleigh lorsque r = 0 (absence de trajet direct) et permet d’identifier un trajet direct et sa prépondérance. Elle est également caractérisée par le coefficient K (paramètre de Rice ) défini par la relation :
![]()
Le paramètre K représente le rapport entre la puissance du trajet direct et la contribution en puissance des trajets secondaires obéissant à une loi de Rayleigh.
Plus le paramètre K est grand, plus le trajet direct a une puissance importante par rapport aux trajets multiples et plus la liaison est dégagée. A l’inverse si le trajet prédominant est faible, (K£ -5 dB) on considère que la loi de Rice s’identifie à une loi de Rayleigh [CCIR, 1990]. La valeur de K dépend de l’environnement (urbain dense, suburbain, rural, etc.).
D’autres lois, telles que celles de Weibull et Nakagami [BRAUN, 1991] permettent également de caractériser l’enveloppe du signal radiomobile.
Afin de déterminer la loi de variation suivie par le signal on applique des tests statistiques par exemple le test de Kolmogorov-Smirnov [BARBOT, 1992] sur ses variations rapides résultant des interférences des ondes reçues.
Connaissant les caractéristiques statistiques du signal (densité de probabilité, fonction de répartition), il est possible de déterminer les paramètres pertinents au fonctionnement d’un système radioélectrique parmi lesquels :
- la probabilité de descendre au-dessous d’un certain niveau. Quand la puissance du signal est inférieure au seuil de bruit toléré par le récepteur (bruit thermique, brouillage, parasites industriels, etc.), le signal est masqué par le bruit. Le récepteur est alors incapable d’interpréter correctement l’information transmise.
- la durée statistique d’un évanouissement. Durant l’évanouissement, les paquets d’informations sont perdus. Les temps de coupure sont d’autant plus long que le mobile se déplace lentement.
Lorsque les différences de temps de parcours des trajets multiples sont importantes, la fonction de transfert n’est plus constante sur toute la largeur du spectre : l’affaiblissement de propagation dépend de la fréquence à laquelle on se place. Le canal est dit sélectif en fréquence.
Une modélisation du canal en large bande est alors indispensable pour évaluer les performances d’une chaîne complète de transmission, concevoir les nouveaux systèmes et assurer la qualité de transmission de signaux numériques.
Le canal radioélectrique est représenté par sa réponse impulsionnelle variable dans le temps, h(t,t ), t étant le retard et t rappelant la dépendance en temps (et donc en espace puisque le véhicule se déplace). Fonction à deux variables, elle traduit les trois caractéristiques du canal : l’affaiblissement, la variabilité (t) et la sélectivité (t ).
Les variables duales, par transformée de Fourrier de t et de t sont respectivement la fréquence et la vitesse Doppler [PARSONS, 1992], [KATTERBACH, 1995].
Le signal de sortie y(t) en fonction du signal d'entrée x(t) est représenté sous la forme d'une équation de convolution dont le noyau de convolution est variable dans le temps :
![]()
où h(t,t ) est la réponse à l'instant t à une impulsion radioélectrique x(t) que l'on aurait émise à l'instant t-t . Elle définit totalement le canal de propagation. Elle permet de distinguer les différents échos en fonction de leurs retards de propagation.
Il est usuel de qualifier la sélectivité du canal par des paramètres déduits du profil moyen de puissance de la réponse impulsionnelle. Les plus utilisés sont le retard moyen, l'étalement des retards, l’intervalle des retards, la fenêtre des retards et la bande de cohérence du canal [FAILLY, 1989].
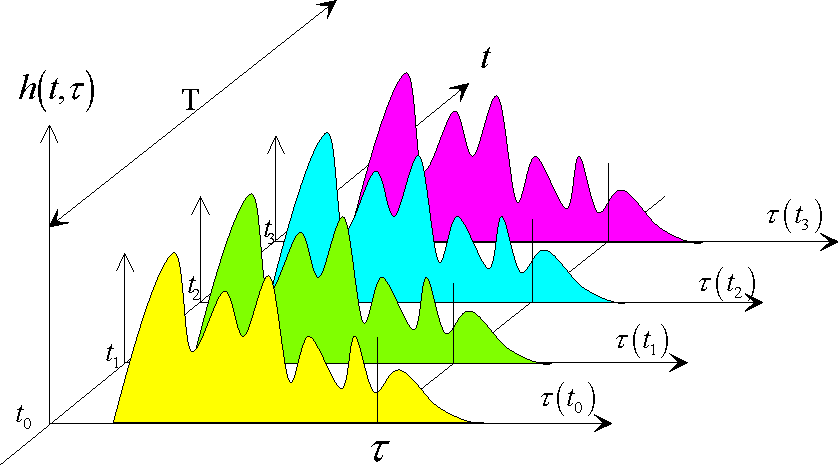
Figure 3 : Représentation schématique de l'évolution temporelle de la réponse impulsionnelle du canal de propagation
4.3.1 – Densité de puissance moyenne
On définit la densité de puissance moyenne P(t ) de la réponse impulsionnelle (" average delay profile ") à partir de h(t,t ) par la relation :

Elle correspond à une moyenne sur une certaine durée T choisie de telle sorte que les réponses impulsionnelles mesurées sont représentables par un processus aléatoire stationnaire et ergodique [LAVERGNAT, 1997].
Le retard moyen est la moyenne des retards pondérés par leur puissance. Il est donné par le moment d’ordre un de la réponse impulsionnelle :

où : t LOS est le temps de propagation en visibilité directe,
t
3 est l' instant où P(t ) dépasse le seuil de coupure pour la dernière fois.Pm est l’énergie totale de la réponse impulsionnelle, définie par la relation suivante :

où :
P(t,t ) est la densité de puissance de la réponse impulsionnelle,
t est le retard en excès,
t 0 est l'instant où P(t ) dépasse le seuil de coupure pour la première fois
4.3.3 – La dispersion des retards
La dispersion des retards ou écart-type des retards pondérés par leur puissance est donné par le second moment de la réponse impulsionnelle :

La dispersion des retards illustre le risque d'apparition d'interférences inter-symboles et les effets perturbateurs que les échos lointains et puissants sont susceptibles d'engendrer.
4.3.4 – L'intervalle des retards
L’intervalle des retards à X dB est défini comme l’intervalle de temps entre l’instant t 1 où l’amplitude de la réponse impulsionnelle dépasse pour la première fois un seuil donné et l’instant t 2 où cette amplitude devient pour la dernière fois inférieure à ce seuil.

Figure : Exemple de profil de retard de puissance ; mise en évidence de l’intervalle des retards à X dB.
4.3.5 – La fenêtre des retards
La fenêtre des retards à y %, est la durée de la portion centrale (t 2-t 1) de la réponse impulsionnelle qui contient y% de l’énergie totale. Les instants t 1 et t 2 sont définis par la relation :
![]()

Figure : Exemple de profil de retard de puissance ; mise en évidence de la fenêtre des retards à y%.
La bande de cohérence (Bcohérence) du canal est définie de la façon suivante. Soit C(t,f) l’autocorrélation de la fonction de transfert (Transformée de Fourier de la puissance de la réponse impulsionnelle).

La largeur de bande de corrélation est définie comme la fréquence pour laquelle |C(t,f)| est égale à x % de C(t,f=0) [PARSONS, 1992]. Elle indique l'amplitude de l'affaiblissement sélectif en fonction de la séparation en fréquence. La bande de corrélation est donc la fréquence à partir de laquelle la fonction d'autocorrélation de la fonction de transfert franchit un seuil donné.
Pour l’analyse des données expérimentales, l’UIT-R recommande d’utiliser des intervalles des retards pour des seuils de 9, 12 et 15 dB en dessous de la valeur crête, des fenêtres des retards pour 50%, 75% et 90% de l’énergie et une largeur de bande de corrélation pour 50% et 90% de corrélation.
La bande de corrélation est reliée à la dispersion des retards par la relation suivante [LEE, 1993] :
![]()
Le canal de propagation est plus ou moins sélectif selon l’environnement dans lequel on se trouve. La forme de la réponse impulsionnelle est également différente selon l’environnement. Sur la réponse impulsionnelle en intérieur des bâtiments, la décroissance de la puissance en fonction des retards est exponentielle alors qu'en petite et micro cellule des trajets à des retards importants se distinguent très nettement. On notera, sur la figure 4, que les échelles de temps ne sont pas les mêmes pour l'environnement intérieur des bâtiments et pour les environnements micro et petite cellule.

De gauche à droite : en intérieur des bâtiments, petite-cellule et micro cellule.
Figure 4. :Exemples de réponses impulsionnelles mesurées dans différents environnements
5 – Les différents modèles de propagation
Devant la demande sans cesse croissante, les opérateurs ont été amenés à densifier leur réseau : ils augmentent le nombre des stations de base et réduisent la taille des cellules. La cellule est la zone couverte par une station de base. On distingue généralement quatre types de cellules (figure 5). Elles schématisent des implantations physiques particulières de l'antenne de la station de base et de sa zone géographique déterminée : leurs caractéristiques sont liées à la position, la puissance, la hauteur de l'antenne de la station de base et à l'environnement géographique.

Figure 5 : Les différents types de cellules
La cellule la plus grande est la macro cellule. Le milieu environnant est en général rural ou montagneux et l’antenne de station de base est positionnée sur un point très élevé. La distance entre la station de base et le mobile peut être supérieure à une dizaine de kilomètres. Cette zone géographique, peu urbanisée, entraîne pour un certain nombre de trajets de délais élevés (jusqu'à 30 m s). De plus, les diffuseurs, étant éloignés et en nombre restreint, engendrent des évanouissements rapides peu prononcés.
Face à l’augmentation croissante du nombre d’utilisateurs en ville principalement, il a fallu diminuer la taille des cellules afin de réduire la distance de réutilisation des fréquences allouées. La plus courante des cellules implantées en ville est la petite cellule. Elle couvre un rayon inférieur à quelques kilomètres et l’antenne de station de base est située au-dessus du niveau des toits. La durée maximale de la réponse impulsionnelle est de 10 m s.
En urbain très dense, la petite cellule est remplacée par des micro cellules ayant un champ d’action de quelques centaines de mètres. Les antennes étant sous le niveau des toits, la propagation des ondes est guidée par les rues. La durée maximale de la réponse impulsionnelle est de 2 m s.
Il y a enfin la pico cellule, de quelques dizaines de mètre de rayon, qui correspond à une communication à l’intérieur même des bâtiments dans lesquels sont placées les antennes des stations de base. La durée maximale de la réponse impulsionnelle est de 1 m s.
A chaque environnement correspond un certain nombre de modèles (théorique, empirique ou statistique, ou semi empirique).
Les modèles théoriques s'appuient sur les lois fondamentales de la physique avec les approximations adéquates. Les modèles empiriques sont basés sur l'analyse statistique d'un grand nombre de mesures expérimentales réalisées en fonction de différents paramètres tels que la fréquence, la distance, de la hauteur effective de l'antenne d'émission, de l'antenne de réception, …etc. Les modèles semi-empiriques combinent une formulation analytique de phénomènes physiques (réflexion, transmission, diffusion , diffraction) et un ajustement des variables à l'aide de mesures expérimentales.
Les modèles de propagation sont utilisés lors de la conception d’une interface radio pour en optimiser les performances et également lors du déploiement des systèmes sur le terrain pour déterminer la couverture radioélectrique.
5.1 - Les modèles macro cellulaires
Les modèles macro cellulaires sont des modèles semi-empiriques généralement fondés sur l’analyse du profil vertical émetteur-récepteur et des obstacles qui s’y trouvent (colline, forêt, etc.). Ils s’appuient généralement sur des données géographiques de type maillé de sol et de sursol. Une mise au point par ajustement de variables est opérée à l’aide de mesures expérimentales du fait de la pauvreté des informations géographiques fournies (estimation de l’occupation du sol sur une maille de 100 m) et de la simplicité des algorithmes de calcul. On distingue deux types de modèles : les modèles ruraux et moyennement urbanisés et les modèles montagneux .
Le modèle rural prend uniquement en compte la coupe de terrain verticale entre l’émetteur et le récepteur pour déterminer les affaiblissements et notamment ceux dus à la diffraction par les obstacles (sol et sursol). Ils permettent d’estimer une couverture radioélectrique avec une précision de l’ordre de 6 à 7 dB d’écart-type sur la moyenne de l’erreur entre valeurs mesurées et valeurs prédites. Les performances peuvent être améliorées en milieu urbain par l’utilisation de données géographiques plus précises. Elles se dégradent lorsque le vallonnement devient important (plus particulièrement en région montagneuse) car les effets des trajets réfléchis deviennent prépondérants.
Le modèle montagneux prend en compte, outre le trajet direct, les trajets réfléchis sur le flanc des montagnes avoisinantes [HASHEMI, 1993a], [KIRLIN, 1994] (cf. figure 6). L’identification des zones de réflexion rend les algorithmes de calcul de l’affaiblissement plus complexes et plus gourmands en temps de calcul.

Figure 6 : représentation schématique d'une configuration montagneuse
L’écart-type des erreurs entre les valeurs mesurées et les valeurs prédites est de l’ordre de 6.4 dB. L’amélioration apportée par ce modèle par rapport au modèle rural est importante, non seulement en haute montagne (Alpes, Pyrénées) mais également en moyenne montagne (Vosges) [BOURDEILLES, 1997].
5.2 - Les modèles petites cellules
L’amélioration des modèles statistiques pour les petites cellules suburbaines et urbaines est obtenue par l’intégration du mode profil et de différents algorithmes de diffraction multiple sur une succession d’arêtes déjà éprouvés dans les modèles de prédiction de champ en environnement rural. Elle permet la prise en compte de l’influence du relief et du sursol par l’intermédiaire d’une base de données géographiques plus ou moins précise.
Le modèle le plus connu est celui élaboré dans le cadre de l’Action COST 231. C’est un modèle semi-empirique 2D adapté aux petites cellules. Le profil se trouve dans le plan de coupe verticale contenant l'émetteur et le récepteur. Il convient plus particulièrement à l’ingénierie du GSM à 900 MHz et du DCS 1800 à 1800 MHz avec une émission à 5 à 15 m au-dessus des toits. La propagation s’effectue principalement par-dessus les toits pour finalement plonger dans la rue où se déplace le mobile. Afin d'étendre le domaine d'application à des configurations de terrain plus marginales (notamment prise en compte du relief), un terme de diffraction supplémentaire au-dessus d'une arête prépondérante (dite arête principale) a été ajouté. Du fait des altitudes (les variations d'altitudes sont rarement très importantes au sein même d'une ville) et des distances mises en jeu, la méthode de Deygout habituellement utilisée à FTR&D a été retenue pour calculer ce terme.
La méthode de calcul de l’affaiblissement est issue des travaux de Walfish et Bertoni sur la diffraction multiple par des arêtes alignées et uniformément réparties [WALFISH, 1988], [XIA, 1992], [MACIEL, 1993], et sur ceux d’Ikegami pour la prise en compte de la dernière diffraction au niveau du mobile [IKEGAMI, 1984]. Deux contributions sont prises en compte : un trajet direct entre la dernière arête et le mobile et un trajet qui se réfléchit sur le bâtiment derrière le mobile dans le plan émetteur-récepteur (cf. figure 7).
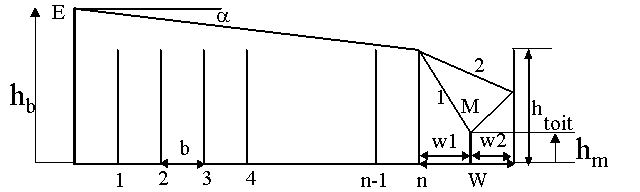
Figure 7 : Profile synthétique du modèle COST 231
Les pertes totales (L) obtenues se décomposent en 4 termes principaux représentant successivement les pertes liées à la distance entre l'émetteur et le récepteur, les pertes liées à la diffraction multiple sur les arêtes, les pertes liées à la dernière diffraction et à la réflexion respectivement sur les immeubles et derrière le mobile et les pertes liées à la diffraction sur une arête principale :
![]()
où :
Afin d'adapter le modèle à des configurations réelles et d'améliorer ses performances, il est en fait construit de manière semi-statistique l'affaiblissement total du modèle s'exprimant donc sous la forme :
![]()
où les Pi désignent les différentes variables géométriques utilisées et où les coefficients a , b , g et ci sont les coefficients obtenus par simple régression linéaire sur un ensemble de mesures données.
5.3 - Les modèles micro cellulaires
La modélisation micro cellulaire repose sur une dualité liée aux faibles distances considérées (quelques centaines de mètres tout au plus) : un calcul en visibilité (LOS, Line Of Sight) et un calcul en non-visibilité (NLOS, Non Line of Sight). En effet, l'émetteur étant situé dans la rue au-dessous du niveau des toits, il s'agit principalement d'une propagation "guidée" le long des rues : soit dans la rue où se trouve l'émetteur (LOS), soit dans les rues adjacentes après le passage d'au moins un coin (NLOS). Nous retrouvons ces deux types de calcul dans la plupart des modèles analytiques 2D (profil) proposés dans la littérature, notamment le modèle à double pente [XIA, 1993] qui considère un affaiblissement en d2 (20log10d) pour la visibilité à faibles distances et un affaiblissement en d4 (40log10d) pour la non-visibilité ou la visibilité à longues distances (combinaison du rayon direct et du rayon réfléchi sur le sol). La position du point de rupture de pente est généralement donnée par la relation suivante :
![]() où hb et hm représente respectivement la hauteur de la station d'émission et celle du mobile.
où hb et hm représente respectivement la hauteur de la station d'émission et celle du mobile.
Dans la pratique, il reste très difficile d'estimer la valeur de la pente en NLOS car elle dépend fortement de l'angle
a entre les rues. Ce sont en fait les travaux sur la Théorie Uniforme de la Diffraction (TUD) [KELLER, 1962], [KOUYOUMJIAN, 1974] qui ont permis d'aboutir à une formulation analytique précise des phénomènes de propagation en zones urbaines [BERTONI, 1994], [BERG, 1995], [JAKOBY, 1995].Le modèle MCG-CNET est un modèle analytique 2´ 2D qui généralise ces deux aspects en effectuant un calcul d'affaiblissement dans le plan horizontal pour les cas où la propagation le long des rues est le phénomène prépondérant [WIART, 1993] et un calcul sur profil dans le plan vertical contenant l'émetteur et le récepteur pour les cas de visibilité ou de non-visibilité mais où la propagation par-dessus les toits devient prépondérante (longues distances, présence de bois ou encore, environnements pavillonnaires où la hauteur moyenne des bâtiments est peu élevée par rapport à la hauteur de l'émetteur...). On a ainsi deux catégories de calcul, le long des rues et sur le profil.
5.3.1 - Calcul le long des rues
Une analyse de la propagation à 900 MHz et 1800 MHz au passage d'un coin de rue par des simulations effectuées à l'aide des méthodes d'électromagnétisme(TUD) a conduit à des expressions analytiques simplifiées des mécanismes de propagation en visibilité, de réflexion et de diffraction en fonction des largeurs de rues origine et destination (respectivement W1 et W2), de la distance de l'émetteur au coin (D), de la distance du coin au récepteur (X), de l'angle a fait par les deux rues etde la fréquence d'émission. L'affaiblissement (Aff) au niveau du récepteur après le passage du coin se décompose de la façon suivante :
![]()
où:
- AffVis est l'affaiblissement en visibilité sur la distance D
![]()
- AffRef est l'affaiblissement dû à la réflexion [WIART, 1993].
![]() avec
avec
- f est la fréquence utilisée,
- D est la distance entre l'émetteur et le coin de rue,
- S représente la pente de la décroissance de la puissance au passage de la rue,
- W1 et W2 sont les largeurs de rue en visibilité et en non visibilité,
- X est la distance du récepteur au coin de rue,
![]()
![]() - f(a ) est une fonction de l'angle a de la rue.
- f(a ) est une fonction de l'angle a de la rue.
- AffDif est l'affaiblissement dû à la diffraction [WIART, 1993].
![]() où
où
![]()

Figure 8 : Cas type du passage d'un carrefour en microcellulaire
Pour déterminer l'affaiblissement entre un émetteur et un récepteur, le modèle MCG-CNET recherche tous les chemins possibles entre le point d'émission et le point de réception. Les contributions apportées par les différents chemins sont sommées en Watts, et la résultante est convertie en décibels.
Lorsqu'il s'agit de prédire un affaiblissement dans un environnement spécifique non typiquement microcellulaire (grandes distances en LOS ou NLOS, grandes places, squares, présence de bois...), un calcul le long des rues devient trop irréaliste et erroné. Il est nécessaire d'introduire un calcul selon un profil. Le principe repose sur le fait que l'onde qui se propage par-dessus les toits ou à travers les arbres est prépondérante devant celle qui se propage le long des rues. Le modèle consiste en :
- l'interprétation d'un profil réel pour se ramener à un calcul de diffraction multiple au-dessus des toits et de diffraction et réflexion au niveau du mobile et de l'émetteur de type Walfisch-Bertoni-Ikegami.
- l'adaptation des formules théoriques habituellement utilisées en petites cellules dans un environnement microcellulaire.
Le principe repose sur le fait que l'onde qui se propage par-dessus les toits ou à travers les arbres est ou devient prépondérante à celle qui se propage le long des rues.
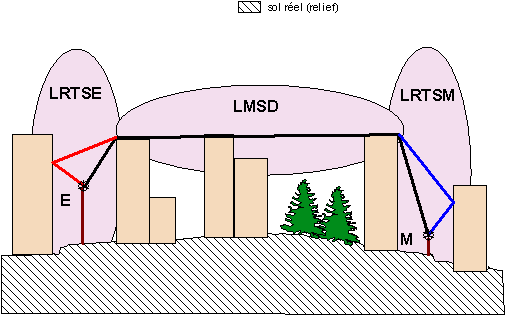
Figure 9 : Profil microcellulaire
Afin d’adapter le modèle à des configurations réelles et pour améliorer ses performances, il est en fait construit de manière semi-statistique, l’affaiblissement total (L0) s’exprimant sous la forme :

Le calcul de l’affaiblissement du modèle fait intervenir :
- un affaiblissement lié à la distance (Ld)
- un affaiblissement de diffraction (LMSD)
- un affaiblissement de diffraction et de réflexion au niveau de l'émetteur (LRTSE)
- un affaiblissement de diffraction et de réflexion au niveau du récepteur (LRTSM)
- un affaiblissement de diffraction sur le MNT de type Deygout (δAdeg)
- un ensemble de variables géométriques notamment liées à la distance de végétation traversée (Pi)
5.4 – Modèle à lancer de rayons
La technique du lancer de rayon est une technique déterministe particulièrement prometteuse. S'appuyant sur des bases de données géographiques très précises et sur une théorie physique, elle est particulièrement bien adaptée pour les environnements urbains et permet d'obtenir des résultats de calculs très riches en informations comme les réponses impulsionnelles. C'est pour ces raisons que, ces dernières années, de nombreux modèles utilisant cette méthode sont apparus, [KURNER, 1993], [LAWTON, 1994], [LIANG, 1998].
Le modèle RAYON développé à FTR&D est un modèle basé sur une technique de lancer de rayons et conçu pour effectuer une recherche systématique des trajets reliant l'émetteur au récepteur faisant intervenir une combinaison des phénomènes physiques réflexions, diffractions horizontales et verticales, pénétration et traversée de végétation dans un ordre et en nombre quelconque et paramétrable. Tous ces phénomènes sont déduits uniquement de leurs valeurs théoriques données par la Théorie Uniforme de la Diffraction (TUD) pour les diffractions et par les formules de Fresnel et Beckmann pour les réflexions.
La méthode classique de lancer de rayons est de lancer, dans toutes les directions, un ensemble dense des lignes directrices à partir de l'émetteur. Chaque rayon représente la partie de l'onde électromagnétique comprise dans un cône autour de cette ligne directrice. Pour des raisons de gain de temps de calcul, certaines hypothèses ont permis de simplifier la géométrie du problème. La figure 9 décrit la démarche effectivement suivie [ROSSI, 1991], [ROSSI, 1992].
Dans un premier temps, seul le plan horizontal est considéré :, la station de base E ainsi que tous les obstacles sont représentés par leur projection verticale sur ce plan. Les rayons sont alors envoyés, à partir de l'émetteur E, à intervalles angulaires réguliers dans le plan. A ce stade, dans l'espace 3D, le rayon ne représente plus un cône autour du rayon mais une tranche verticale de l'espace. Quand un rayon rencontre une limite de bâtiment (point 1 sur la figure 9), il a la possibilité soit de passer par-dessus, soit d'être réfléchi. Les deux cas sont explorés en créant, à partir de ce point, deux branches : l'une poursuit son chemin en ligne droite, l'autre est orientée dans la direction de réflexion spéculaire. La même duplication est produite à chaque rencontre du rayon avec un obstacle jusqu'à ce que le rayon soit trop affaibli ou sorte du cadre des données du terrain. Quand le rayon rencontre un récepteur R, la troisième dimension est alors considérée en dépliant le rayon suivant ses coordonnées curvilignes sur la carte(cf. figure 9), les immeubles de réflexion y sont représentés par une simple barre verticale. Le trajet du rayon correspond au plus court chemin entre la base et le mobile qui passe au-dessus des bâtiments de diffraction. Une fois cette coupe obtenue, le calcul rigoureux de la liaison sur l'atténuation est possible. La puissance moyenne reçue au récepteur est la résultante des puissances de chacun des rayons parvenant à ce point.

Figure 9 : Principe du lancer de rayon (modèle Rayon)
La figure 10 donne un exemple de l'ensemble des rayons reliant un émetteur et un récepteur dont la puissance est dans une dynamique de 20 dB.

Figure 10 : Rayons diffractés et réfléchis entre un émetteur (E) et un récepteur (R) (modèle rayon)
5.5 - Modèle de pénétration
L'affaiblissement de pénétration dans un bâtiment est défini comme étant la perte de puissance subie par le champ électromagnétique entre l'extérieur autour du bâtiment et une ou plusieurs positions à l'intérieur de l'immeuble. Il est calculé en comparant le champ extérieur et le champ dans les pièces de l'immeuble où se trouve le mobile récepteur. Les modèles d'affaiblissement, intégrés aux outils de prédiction de champ, se doivent de prendre en compte l'environnement proche du bâtiment étudié.
Les paramètres affectant les valeurs d'affaiblissement de pénétration sont multiples et leurs effets s'entremêlent la plupart du temps. Parmi ces nombreux paramètres on distingue généralement les paramètres classiques suivants :
- l'environnement proche. On distinguera les quartiers avec de grandes tours plus ou moins dégagées les unes des autres et les quartiers plus traditionnels comportant des bâtiments de hauteur moyenne,
- la profondeur de réception dans les bâtiments. Le champ décroît lorsque le mobile se déplace de la façade vers le fond d'une pièce à l'intérieur du bâtiment. L'effet des inhomogénéités de la façade décroît lorsque l'on se rapproche du fond de la pièce. Les ondes pénètrent plus facilement dans l'immeuble par les parties vitrées que par les murs en brique et par conséquent certains trajets sont plus ou moins affaiblis, voir occultés. Les façades vitrées présentent en général un affaiblissement de pénétration de 6 dB inférieur par rapport aux façades non vitrées [RAPPAPORT, 1994]. Au fond du bâtiment l'affaiblissement est plus important mais aussi beaucoup plus homogène.
- l'angle d'incidence. Il agit sur les coefficients de réflexion et de transmission à travers une surface.
- la hauteur de réception plus communément appelée "effet d'étage". De façon générale cet effet d'étage s'exprime sous la forme d'une diminution de l'affaiblissement de pénétration ou d'un gain de puissance relatif par rapport à l'étage inférieur. La base de calcul est donc l'affaiblissement de pénétration au rez de chaussée déterminé par rapport au champ extérieur. En petite cellule, le gain de puissance observé classiquement est de l'ordre de 2 à 3 dB par étage à 900 et 1800 MHz. Cependant la forte diversité des situations provoque une dispersion des gains par étage; des valeurs de l'ordre de 4 à 7 dB ont déjà été mesurées en pratique [GAHLEITNER, 1994]. Les étages de la partie inférieure sont éclairés par des rayons subissant nombre de réflexions et diffractions sur les toits et dans la rue alors que les étages de la partie supérieure bénéficient d'un éclairement généralement beaucoup plus fort, parfois même direct. Les conséquences sur la pénétration sont donc variées [RAPAPPORT, 1994] et [WALKER, 1983].
- la distance entre l'émetteur et le récepteur, lorsque le bâtiment abritant le mobile est en visibilité de l'antenne émettrice. L'affaiblissement de pénétration est alors tributaire de la distance par la loi de propagation en espace libre.
- la hauteur de l'antenne d'émission,
- la fréquence,
- le type de matériaux traversés. Les traversée des matériaux provoque un affaiblissement des ondes électromagnétique, de l’ordre de 4 dB (bois) à 10 dB (béton) [COST231, 1999].
Différentes techniques de mesures ont été développées pour caractériser l’affaiblissement de pénétration dû à des composants du bâtiment. On peut notamment citer la méthode avec deux chambres réverbérantes [FOULONNEAU, 1996].
Les modèles les plus classiques s'inspirent du modèle de Motley Keenan [MOTLEY, 1988] utilisé en propagation à l'intérieur des bâtiments. Ils prévoient l'affaiblissement de pénétration en fonction de paramètres tels que :
- la distance entre l'émetteur et le mur extérieur du bâtiment où se trouve le récepteur,
- la distance entre le mur extérieur et le récepteur,
- le nombre de parois internes coupées par le profil,
- l'effet d'étage,
- l'affaiblissement du mur extérieur du bâtiment,
- l'affaiblissement des parois internes.
L’affaiblissement de propagation (L) s’exprime par une somme des pertes en espace libre (L0), des pertes dues aux obstacles traversées par le rayon direct (dalles, murs, portes, fenêtres), d’une constante (Lc) [MOTLEY, 1988]. La base de données peut différencier les différents obstacles auxquels est associée une valeur particulière d’affaiblissement. C’est le modèle le plus utilisé.
![]()
où :
Nj est le nombre de murs traversés de type j,
Lj sont les pertes dues aux murs de type j,
N est le nombre de types de murs différents,
Nf est le nombre de dalles traversées,
Lf sont les pertes par dalle.
5.6 – Modèles à l'intérieur des bâtiments
La propagation à l’intérieur des bâtiments dépend du type d’environnement dans lequel on se trouve : dense (bâtiments de type bureau), ouvert (bâtiments de type bureau, de grands bureaux pouvant accueillir plusieurs personnes, large (bâtiments ayant de très grandes pièces tels qu'entrepôts, aéroports, gares) et corridor (l’émetteur et le récepteur étant situés dans le même couloir). Elle est également multi-trajets : les mécanismes prédominants sont la réflexion, la transmission, la diffraction et la diffusion [HASHEMI, 1993b], [VALENZUELA, 1997].
On distingue les modèles profil en distance, les modèles profil de type " Motley-Keenan " [KEENAN, 1990] et les modèles multi-rayons encore appelé modèle de couloir.
Dans le cas des modèles profil en distance, les paramètres pris en compte sont la fréquence et la distance entre l’émetteur et le récepteur. Deux modèles sont proposés, le premier [COST231, 1999] suppose une dépendance logarithmique de l’affaiblissement en fonction de la distance, le second suppose une dépendance linéaire [COST231, 1999]. Les deux modèles sont utilisables pour des situations de non-visibilité.
Les modèles de type Motley-Keenan s’appliquent aux cas de non-visibilité en environnement dense (bureau). L’affaiblissement de propagation (L), tout comme en pénétration, s’exprime par une somme des pertes en espace libre (L0), des pertes dues aux obstacles traversées par le rayon direct (dalles, murs, portes, fenêtres), d’une constante (Lc) [MOTLEY, 1988]. La base de données peut différencier les différents obstacles auxquels est associée une valeur particulière d’affaiblissement. C’est le modèle le plus utilisé.
![]()
où : Nj est le nombre de murs traversés de type j,
Lj sont les pertes dues aux murs de type j,
N est le nombre de types de murs différents,
Nf est le nombre de dalles traversées,
Lf sont les pertes par dalle.
Dans la technique du lancer de rayons, les modèles proposés sont généralement en 3 dimensions car le milieu de propagation est dense. Développés par de nombreux auteurs [RAPPAPORT, 1994], [SEIDEL, 1994], [CICHON, 1994], ils conduisent à des résultats encourageants [RAPPAPORT, 1994]. Ils constituent de bonnes références pour la mise au point de modèle multi-rayons mais restent d’usage restreint en ingénierie en raison d’un temps de calcul important.
La technique du tracé de rayons consiste à construire des rayons à l’aide de la théorie des images. Elle permet de prendre en compte facilement les mécanismes de propagation (réflexions multiples, diffractions, etc.). Cette technique a été utilisée par de nombreux auteurs [MC KOWN, 1991], [COST231, 1999], [VALENZUELA, 1994], [JENVEY, 1994], [LAURENSON, 1993].
Les deux autres approches, la méthode des différences finies [MURCH, 1994], [LAUER, 1994], et celle de l’approximation de Tayleig-Gans [LU, 1993], utilisent des relations dérivées des équations de Maxwell. Le milieu de propagation est maillé. Le champ radioélectrique se propage, itération après itération, dans l’espace entourant l’émetteur. Le temps de calcul est très important car le pas de maille doit être très inférieur à la longueur d’ondes (de l’ordre de l /8). Toutefois on ne dispose pas actuellement de résultats représentatifs de leurs performances, les méthodes étant très récentes.
Les modèles à rayons sont des modèles déterministes. Ils reposent sur une connaissance précise de la réalité et nécessitent de disposer de bases de donnée géographique de type Contours de Bases ou intérieur des bâtiments. Ils permettent de prédire les différents trajets de propagation dans une configuration donnée. Après ajustement à la bande de fréquence considérée, ces modèles permettent également par simulation de réaliser des études paramétriques pour analyser par exemple l'influence des diagrammes d'antennes ou des caractéristiques des matériaux ce qui est beaucoup plus économique que la réalisation de multiples campagnes de mesures.
Nous donnons ci-dessous, à titre d'illustration, deux exemples de tracé de rayons : l'un à l'extérieur des bâtiments, l'autre à l'intérieur des bâtiments.
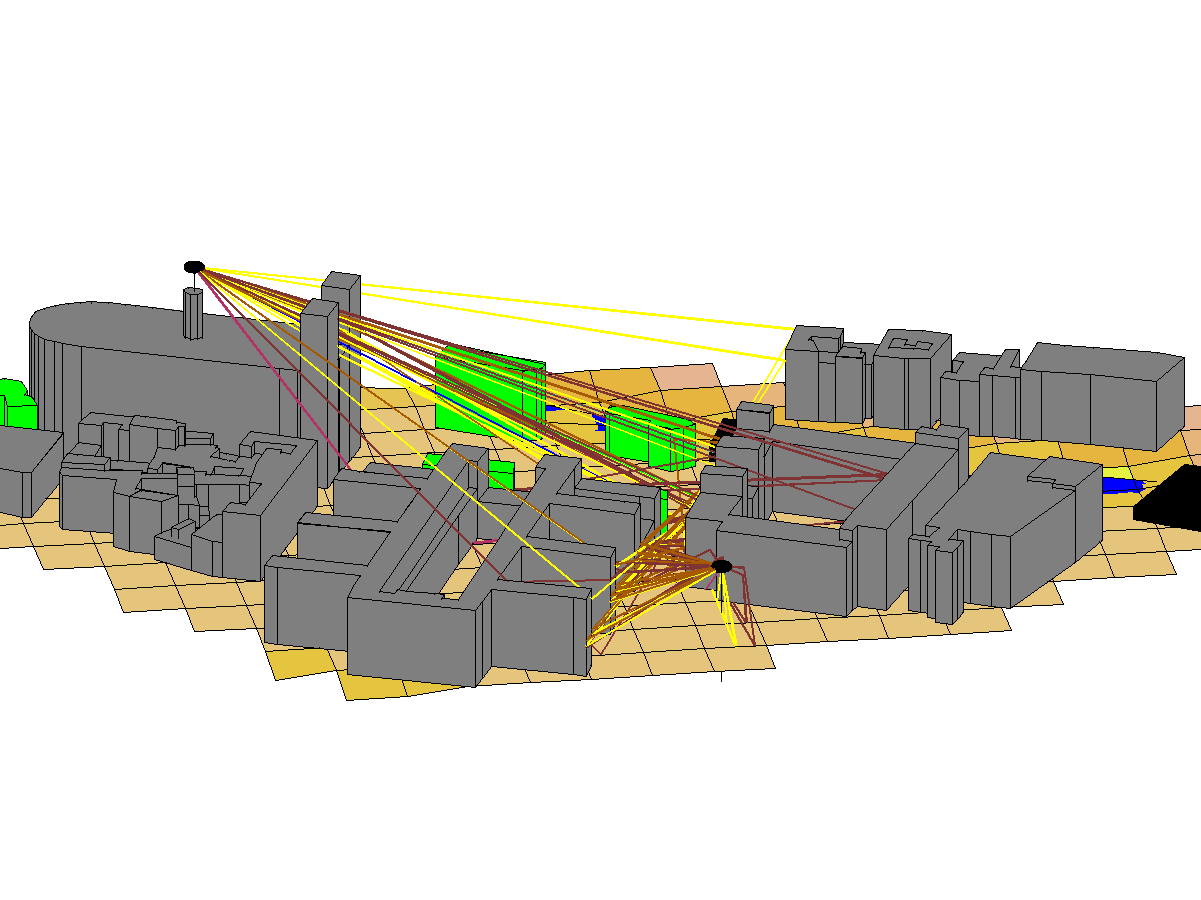
Figure 11 : exemple de tracé à l'extérieur des bâtiments
Figure 12 : exemple de tracé à l'extérieur des bâtiments
Après avoir décrit très succinctement les ondes électromagnétiques nous avons présenté les différents mécanismes de propagation (réflexion, diffusion, transmission, diffraction, …., etc) ainsi que les propriétés du canal (affaiblissement, variabilité, sélectivité). La sélectivité du canal est qualifiée à partir de paramètres déduits du profil moyen de puissance de la réponse impulsionnelle (retard moyen, étalement, intervalle et fenêtre des retards, bande de cohérence). Ces différents paramètres permettent de caractériser le milieu de propagation.
La caractérisation du canal permet en outre d’analyser les nouvelles techniques. L’utilisation d’antennes adaptatives et l’accès multiple à répartition spatial (SDMA, Space Division Multiple Access) font actuellement l’objet de nombreuses études car elles devraient permettre d’accroître significativement les capacités des systèmes existants et celles de la troisième génération [SWALES, 1990]. Le principe est de focaliser le gain de l’antenne de la station de base vers un mobile et ainsi, avec plusieurs pinceaux, de traiter plusieurs mobiles spatialement séparés mais pouvant utiliser le même intervalle de temps et la même fréquence. La conception de tels systèmes requiert des informations supplémentaires sur les directions d’arrivée des signaux. En effet, si en l’absence de trajets multiples l’énergie provient d’une seule direction celle de l’émetteur (techniques de " beam-forming " ), dans le cas d’une zone urbaine, les différents trajets multiples ne sont pas tous dans la même direction.
Dans la dernière partie sont présentés les différents modèles pour le déploiement des systèmes mobiles et objets communicants dans différents environnements (rural, montagneux, suburbain, urbain, intérieur des bâtiments) et différents types de cellule (macro-cellulaire, petite cellule, micro-cellulaire et pico-cellulaire) en nous limitant essentiellement aux modèles à bande étroite. De plus amples détails concernant ces différents modèles peuvent être obtenus dans la littérature [LAGRANGE, 2000].Les modèles large bande à savoir les modèles à trajet (COST 207, ATDMA [RACE, 1994], IUT-R, CSELT), à représentation (modèle de canal enregistré en propagation déterministe) et géométriques n'ont pas été abordés.
[BARBOT, 1992] BARBOT J.P., LEVY A.J., BIC J.C.; "Estimation of fast fading distribution functions", Com. URSI Commission F Open Symposium, 1992
[BERG, 1995] BERG J-E.; "A recursive method for street microcell path loss calculations", PIMRC'95, Toronto, Canada, pp.140-143, 1995.
[BERTONI, 1994] BERTONI H.L., HONCHARENKO W., MACIEL L.R., XIA H.H.; "UHF propagation prediction for wireless personal communications", Proceeding of the IEEE, Vol. 82, n° 9, PP.1333-1359, 1994.
[BOITHIAS, 1893] BOITHIAS L.; "Propagation des ondes radioélectriques dans l'environnement terrestre", Dunod, 1983.
[BOURDEILLES, 1997] BOURDEILLES J-F.; "Modélisation de la propagation pour l'ingénierie radio des systèmes de communications avec les mobiles", SEE : Propagation électromagnétique dans l'atmosphère du décamétrique à l'angström, rennes, pp.115-120, 7-9 octobre 1997.
[BRAUN, 1991] BRAUN W.R., DERSCH U.; "A physical mobile radio channel", IEEE Transactions on Vehicular Technology, Vol. 40, n°2, pp.472-482.
[CICHON, 1994] Cichon D.J., Wiesbeck W., " Indoor and outdoor propagation modelling in pico cells ", PIMRC’94, Personal Indoor Mobile Radio Communications, Sept. 1994.
[CLARKE, 1968] Clarke R.H., " A statistical theory of mobile-radio reception ", B.S.T.J. p.957-1000, août 1968.
[CNET/CSELT Cooperation, 1998] CNET/CSELT Cooperation, Data transmission on DECT standard, "Definition of common propagation models, regeneration scheme and performance evaluation criteria for the aligment of the two radio link simulators, march 1998.
[COST 259, 2000] COST 259, Web informations : http://www.lx.it.pt/cost259.
[COST231, 1999] COST 231, " Evolution of land mobile radio (including personal) communications, Final report, Information, Technologies and Sciences, European Commission, 1999.
[CROCHIERE, 1981] Crochière R.E, Rabiner L.R., "Interpolation and decimation of digital signals – a tutoral review", Proceedings of the IEEE, Vol. 69, n° 3, pp. 300-331, march 1981.
[FAILLY,1989] Failly M., " Final Report of COST 207, Digital Land Mobile Radio Communications ", CEE Luxembourg, 1989.
[FOULONNEAU, 1996] Foulonneau B., Gaudaire F., Gabillet Y. : " Measurement method of electromagnetic transmission loss of building components using two reverberation chambers ", Elect. Letters, 7, Vol .32, N°23, p.2130-2131, 1996.
[GAHLEITNER, 1994] Gahleitner R., Bonek E., " Radio waves penetration into urban buildings in small cell and microcells ", Technische universität Wien, Vienna, Austria, Preceedings Vehicular Technology Conference, Stockholm, p. 887-891, june 1994.
[GFELLER, 1979] GFELLER F.R., BAPST U.R.S.; "Wireless in-house data communication via diffuse infrared radiation" Proceeding of the IEEE, Vol, 67, n° 11 1979.
[HASHEMI, 1993a] Hashemi H., Sajjadi B.A., Tabatabaei V., "Practical design considerations for digital mobile radio systems operating in the mountainous terrain ", 43th IEEE Vehicular Technology Conference, Vehicular Technology Conference, Secaurus, p. 53-56, 1993.
[HASHEMI, 1993b] Hashemi H., "The Indoor Radio Propagation Channel", Proceedings of the IEEE, Vol. 81, N° 7, p. 943-968, 1993.
[Hata, 1980] Hata M., " Empirical formula for propagation loss in land mobile radio service ", IEEE Transactions on Vehicular Technology vol. 29, p. 317-325, 1980.
[Ikegami, 1984] Ikegami F., Yoshida S., Takeuchi T., Umehira M., " Propagation factors controlling mean field strength on urban streets ", IEEE Transactions on Antennas and Propagation, vol. 32, n°8, p. 822-829 août 1984.
[IUT-R, 1996] International Telecommunication Union Study Groups "Guidelines for evaluation of radio transmission technologies for IMT-2000/FPLMTS", FPLMTS.REVAL, Question ITU-R, document 8/29-E, june 1996.
[JAKOBY, 1995] Jakoby R., Liebenow U., " Modelling of radiowave propagation in microcells ", Proc. Intern. Conference on Antennas and propagation , ICAP, Eindhoven, The Netherlands, p. 377-380, 1995.
[JENVEY, 1994] Jenvey S. , " Ray optics modelling for indoor propagation at 1.8 GHz. Proceeding of the IEEE 44th Vehicular Technology Conference, Stockholm Sweden, June 1994.
[KATTENBACH, 1995] Kattenbach R., Fruchting H., " Calculation of system and correlation functions for WSSUS channels from wideband measurements ", Frequenz 49, 3-4, p. 42-47, 1995.
[KEENAN, 1990] Keenan J.M., Motley A.J., " Radio coverage in Buildings ", British Telecom Technol. J., vol 8, n°1, Jan. 1990.
[Keller, 1962] Keller J.B., " Geometrical theory of diffraction" , JOSA vol. 52, p. 116-130, 1962.
[KIRLIN, 1994] Kirlin R.L., Du W., Cui Y., Robertson G., Zhang Y., Driessen P.F.,
"Mesasured 900 Mhz complex impulse responses in mountainous terrain : Relationship to topographical map data", Wireless Personal Communications, Trends and Challenges, Kluwer Academic Publishers, 1994.
[KOUYOUMJIAN, 1974] Kouyoumjan R.G., Pathak P.H., " A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface", Proc IEEE vol. 62, n°11, p. 1448-1461, Nov. 1974.
[KURNER, 1993] Kurner T., Cichon D.J., Wiesbeck W., "Concepts and Results for 3D Digital Terrain Based Wave propagation Models : an overview ", IEEE Trans. Selected Areas in Com., Vol. SAC 11, N° 7, Sept. 93, p. 1002-1012.
[LAGRANGE, 2000] LAGRANGE X.;"Les réseaux mobiles"; Chapitre 2 : Propagation radioélectrique (SIZUN H., BIC J.C.), Réseaux et Télécoms, Information-Commande-Communication, HERMES, 2000.
[LASPOUGEAS, 2000] Laspougeas P., Pajusco P., Bic J.C., "Radio propagation in urban small cells environment at 2 GHz : Experimental spatio-temporal characterization and spatial wideband channel model", Proc. IEEE Vehicular Technology Conference (VTC'2000), Boston, 2000.
[LAUER, 1994] Lauer A., Bahr A., Wolff I., " FDTD simulations of indoor propagation ", ", Proceedings of the 44th Vehicular Technology conference, Stockholm, Sweden, June 1994.
[LAURENSON, 1993] Laurenson D.I., McLaughlin S., Sheikh A.U.H., " The application of ray tracing and the GTD to indoor channel modelling ", IEEE Conf. GLOBECOM’93, Houston, USA, Dec 1993.
[LAVERGNAT, 1997] Lavergnat J., Sylvain M., " Propagation des ondes radioélectriques ", Collection Pédagogique de Télécommunication, MASSON, 1997.
[LAWTON, 1994] Lawton M.C., Macgeehan J.P., " The application of a deterministic ray launching for the prediction of radiochannel characteristics in small cell environment " , IEEE Transactions on Vehicular Technology, Vol 43 N° 4, p. 955-969, Nov 1994.
[LIANG, 1998] Liang G., Bertoni H.L., " A new approach to 3D ray tracing for propagation prediction in cities ", IEEE Transactions on Antennas and Propagation, vol. 46, n° 6, june 1998.
[LU, 1993] Lu Y.E., " Site precise radio wave propagation simulations by time domain finite difference methods ", Proceedings of the 43th Vehicular Technology Conference, Meadowlands, USA, May 1993.
[Maciel, 1983] Maciel L.R., Bertoni H.L., Xia H.H., " Unified approach to prediction of propagation over buildings for all ranges of base station antenna height ", IEEE Transactions on Vehicular Technology, vol. 42, n°1, février 1993.
[Mc KOWN, 1991] Mc Kown J.W., Hamilton R.L., " Ray tracing as a design tool for radio networks ", IEEE Network Magazine, Nov . 1991.
[McNAMARA, 1990] McNAMARA D.A., PISTORIUS C.W.I., MALHERBE J.A.G.; The Uniform Geometrical Theory of diffraction, Artech, House, London, 1990.
[METAMORP, 2000] Metamorp Project, "Description of the modeling method", Deliverable C2/1, 2000 (http://www.nt.tuwien.ac.at/mobile/projects/METAMORP/en/.
[MOTLEY, 1988] Motley A.J., Keenan J.M., " Personnal communication radio coverage in building at 900 MHz and 1700 MHz ", Electronics Letters, Vol 24, N°12, June 1988.
[MURCH, 1994] Murch R.D.., Cheung K.W., Fong M.S., Sau J.H.M., Chuang J. CL. "A new approach to indoor propagation prediction ", Proceedings of the 44th Vehicular Technology conference, Stockholm, Sweden, June 1994.
[PARSONS, 1992] Parsons J.D., " The mobile radio propagation channel " Pentech Press Publishers, 1992.
[RACE, 1994] RACE ATDMA Project, "Channel models Issue 2", R084/ESG/CC3/DS/029/b1, Ed. R. GOLLREITER, May 1994.
[RAPPAPORT, 1994] Rappaport T.S., Sandhu S. " Radio Wave Propagation for Emerging Wireless Personal Communication Systems ", IEEE Antennas and Propagation Magazine Vol. 36, No. 5, p.14-23 , Oct. 1994.
[ROSSI, 1991] Rossi J.P., Bic, J-C., Levy A.J., Gabillet Y., Rosen M., " A ray launching method for radio-mobile propagation in urban area ", IEEE Antennas and Propagation Symposium, London (Ont.), Vol. 3, p. 1540-1543, June 1991.
[ROSSI, 1992] Rossi J.P., Levy A.J., " A ray model for decimetric radio-wave propagation in an urban area ", Radio Science, Vol. 27 N°6, p 971-979, Nov.-Dec. 1992.
[ROSSI, 1997] Rossi J-P., Barbot J-P., Levy A.J., " Theory and measurement of the angle of arrival and time delay of UHF radiowaves using a ring array ", IEEE Transactions on Antennas and Propagation, Vol. 45, n° 5, p. 876-884, may 1997.
[SIAUD, 1996] Siaud I., A digital signal processing approach for the mobile radio propagation channel simulation with time and frequency diversity applied to an indoor environment at 2.2 GHz", Personal indoor mobile radio communications conference, PIMRC'96, Taiwan, 15-18 october 1996.
[SIAUD, 1997] Siaud I., "A mobile propagation channel model with frequency hopping based on a digita signal processing and statistical analysis of wideband measurements applied in micro and small cells at 2.2 GHz", IEEE Vehicular technology Conference, Phoenix, AZ, Vol. 2, pp. 1084-1088, 4-7 may 1997.
[SIAUD, 1997] siaud I., "Simulation du canal de propagation radiomobile en environnement urbain pour l'étude des performances des systèmes de communication de 3iéme génération avec diversité de fréquence", 3 ièmes journées d'étude, "Propagation électromagnétique dans l'atmosphère du décamétrique à l'angström, pp. 277-282, 7-9 octobre 1997.
[SEIDEL, 1994] Seidel S.Y., Rappaport T.S., " Site-specific propagation prediction for wireless in building personal communication system design " IEEE Transactions on Vehicular Technology, Vol 43, N°4, Nov 1994.
[SWALES, 1990] Swales S.C., Beach M.A., McGeenham J.P., " The performance enhancement of multibeam adaptative base stations antennas for cellular land mobile radio systems ", IEEE Trans. Veh. Tech. Vol 39, n°1, Feb 90, p.56-67, 1990.
[VALENZUELA,1994] Valenzuela R.A., " Ray tracing prediction of indoor radio propagation ", PIMRC’94, Personal Indoor Mobile Radio Communications, Sept. 1994.
[VALENZUELA, 1997] Valenzuela R., Landron O., Jacobs, D.L. : " Estimating Local Mean Signal Strength of Indoor Multipath Propagation " , IEEE Transactions on Vehicular Technology , Vol. 46, N°1, p. 203-121, 1997.
[Walfisch, 1988] Walfish J., Bertoni H.L., " A theoretical model of UHF propagation in urban environments ",IEEE Antennas and Propagation, vol. 36, n°12, p. 1788-1796, déc 1988.
[WALKER, 1983] Walker E.H.," " Penetration of Radio Signals into Buildings in the Cellular Radio Environment ", The Bell System Technical Journal, v. 62, n. 9, p.2719-2730, Nov. 1993.
[Wiart, 1993]Wiart J., Marquis A. , Juy M., " Analytical Microcell path loss model at 2.2 GHz ", PIMRC'93, Yokohama, September 8-11, 1993.
[Xia, 1992] Xia H.H., Bertoni H.L., " Diffraction of cylindrical and plane waves by an array of absorbing half-screens " , IEEE Antennas and Propagation, vol. 40, p. 170-177, n°2, février 1992.
[Xia, 1993] Xia H.H., Bertoni H.L., Radio propagation characteristics for line-of-sight microcellular and personal communications, IEEE Antennas and Propagation, vol. 41, n°10, Oct. 1993.
[YANG, 2000] YANG, H., LU C.; "Infrared wireless LAN using multiple optical sources", IEE Proc. OptoElectron., Vol. 147, n°4, 2000.