

Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
version à télécharger (francais
+anglais) : recepteur.zip
(189ko)
| Introduction |
On envisage de réaliser un système qui permet la réception d’un grand nombre de messages m1(t),…,m2(t) (stations) modulés à des fréquences porteuses de valeurs différentes, espacées d’une quantité constante D (f).
Le système de réception couvre
une bande de fréquences B=![]() .
.
Dans un premier temps nous allons effectuer une
étude préliminaire théorique du système de réception
hétérodyne qui nous permettra de comprendre le principe et les
avantages d’un tel système ; Lors de cette étude nous
pourrons déterminer les différents paramètres utilisés
ultérieurement.
On simulera ensuite la réception hétérodyne à
l’aide des outils de communication fournis par
l’utilitaire Simulink de Matlab. On travaillera en
modulation de fréquence MF.
Enfin nous mettrons en oeuvre un récepteur
fonctionnant en temps réel utilisant les capacités d’un
DSP piloté à partir de Simulink.
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Etude
préliminaire : principe du récepteur hétérodyne |
Le schéma bloc
présenté en figure 1 représente le système classique de
réception d’un message mk(t) de largeur de bande
bk modulé à une fréquence fk.

Figure I.1 Système de
réception
Pour recevoir plusieurs messages, il faudrait théoriquement que le récepteur contienne autant de démodulateurs que de fréquences porteuses différentes. On conçoit que cette solution est très vite irréalisable dès lors que le nombre de stations est important. Pour résoudre cette difficulté, il existe une technique qui au lieu d’adapter le démodulateur à la fréquence du signal à moduler, adapte le signal à un démodulateur fixe. On réalise cette opération en ramenant tous les signaux à recevoir autour d’une fréquence fixe, dite fréquence intermédiaire. Cette technique permet donc d’utiliser le même circuit de démodulation. C’est le récepteur hétérodyne.
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Modulation d’Amplitude Sans Porteuse |
Dans un premier temps on reçoit des messages sur le canal de
transmission ayant subi une modulation d’amplitude sans
porteuse (MASP).
Expression du signal modulé: ![]()
Le signal analytique associé s'écrit: ![]()
où ![]()
soit ![]()
Enveloppe complexe associée au signal modulé: ![]()
avec ![]()
soit ![]()
De là on trouve la forme de la densité spectrale de puissance: ![]()
On a ![]()
et ![]()
Soit ![]()
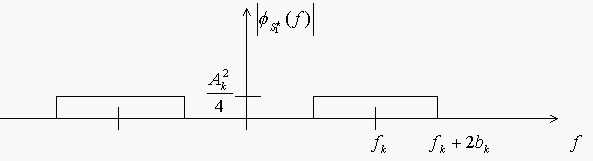
Figure I.1.1 Densité spectrale du signal modulé
Calculons maintenant ![]() , spectre du signal
, spectre du signal ![]() en fonction du spectre de
en fonction du spectre de ![]() :
:


Figure I.1.2 Spectre du signal à l’entrée du filtre2
Ainsi on peut représenter la densité spectrale de puissance ![]() du signal
du signal ![]() en fonction de la densité spectrale de puissance
en fonction de la densité spectrale de puissance ![]() :
:

Figure I.1.3 Densité spectrale de puissance du signal à
l’entrée du filtre2
Grâce à un filtre 2 passe-bande on ne va conserver que 2
parties sur les quatre du spectre du signal ![]() ,
le signal est près &aecute; être démodulé.
,
le signal est près &aecute; être démodulé.
![]()
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Démodulation |
On retire le filtre 2 de la
chaîne de réception. On envoie alors le signal s2(t)
à l’entrée du récepteur, constitué principalement
d’un filtre ‘filtre 3’ et d’un démodulateur.
Le filtre 3 est un filtre passe-bande de largeur fixe B, centré
autour d’une fréquence fixe fI. Ce démodulateur
est conçu pour fonctionner à la fréquence intermédiaire fI.
On choisit fI = fosc-
fk pour démoduler le signal modulé à la fréquence
fk. En effet à la sortie de l’oscillateur local
le spectre du signal est renvoyé autour des fréquences (fosc-
fk) et son contraire (-fosc+ fk).
Un dispositif classique de
démodulation pourrait être de la forme :

Figure I.2.1 Démodulateur

A la sortie du passe-bas : ![]()
Lorsqu’on reçoit un signal
situé dans le domaine spectral autour de la fréquence porteuse
f1 on doit caler fosc de telle sorte que fosc-
f1=fI où fI est la fréquence
de démodulation fixe.
Remarque : Si fI
est mal choisie on peut avoir fosc- fk dans
la bande ![]() et donc
il peut y avoir des interférences avec une autre station.
et donc
il peut y avoir des interférences avec une autre station.
On veut donc : 
On prendra fI au
milieu de la bande ![]() .
.
Si on effectue une démodulation
synchrone et cohérente du signal ![]() on obtient en sortie du récepteur le
signal
on obtient en sortie du récepteur le
signal ![]() en
utilisant pour le filtre 4 un filtre passe-bas de largeur
en
utilisant pour le filtre 4 un filtre passe-bas de largeur ![]() .
.
L’intérêt d’un tel
système de réception est qu’avec un seul démodulateur il
est possible de recevoir des messages modulés à différentes
fréquences de porteuse. Il suffit de faire varier fosc
(ex : un potentiomètre permettrait de réaliser cette
opération).
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Modulation de Fréquence |
On désire concevoir un système
de transmission en radiodiffusion MF basé sur le principe du
récepteur hétérodyne développé précédemment.
Le système de radiodiffusion MF
couvre une bande de fréquences [88MHz,108MHz]. La largeur de
bande B du filtre 3 peur varier entre 200kHz et 250kHz. Le signal
est de largeur de bande b=15kHz.
On choisit fI au milieu
de la bande du système de radiodiffusion soit fI=98MHz.
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Simulation sous
Simulink |
On s’est servi des
modulateurs et démodulateurs en bande transposée de la boîte
à outils communication de Simulink. Tous les éléments sont de
type numérique car dans la troisième partie nous utiliserons
une carte d’acquisition qui contient un convertisseur
analogique-numérique. Nous serons donc amenés à travailler sur
des signaux numériques.

Figure II.1.1 Modèle du
récepteur hétérodyne
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Résultats |
Pour la simulation nous avons
utilisé les valeurs de fréquence d’échantillonnage et de
modulation beaucoup plus faibles que celles utilisées en
pratique. Nous avons effectué la simulation en utilisant une
source sinusoïdale. Pour faciliter la visualisation, nous avons
pris une fréquence de modulation relativement faible (proche de
la bande passante du signal). Ainsi nous pouvons observer sur le
même graphique la source, le résultat de la modulation et le
signal démodulé.

Figure II.2.1 Modulation et
démodulation du signal
Sur la figure II.2.1, on remarque
que le signal en sortie du système correspond au signal initial
avec un petit temps de retard dû au temps de réponse du
démodulateur.

Figure II.2.2 Filtrage
passe-bande du signal s2(t)
Nous avons représenté sur
la figure II.2.2 le résultat du filtrage passe-bande entrée du
démodulateur. On constate une différence de fréquence entre la
gauche et la droite de la figure : on a récupéré un
signal propre modulé à la fréquence intermédiaire fI.
Introduction - Principe
du récepteur hétérodyne - MASP
- Démodulation - FM
Simulation - Synthèse
du modèle - Conclusion
| Conclusion |
Quelques remarques
sur le système :
L’élaboration d’un tel système demande une
bonne connaissance des éléments utilisés.
Teentrée et Tesortie sont les périodes d’échantillonnage respectivement du signal en entrée du modulateur et en sortie du modulateur.
Le paramètre en Hz/V (que nous appellerons FV dans la suite) indique la variation de fréquence du signal modulé en fonction du signal d’entrée.
ap sera l’amplitude du signal modulé et fp sa fréquence centrale.
Expression des signaux en entrée (m(t)) et en sortie (s(t)) du modulateur :
![]()
On a donc en sortie une sinusoïde d’amplitude ap et de fréquence fp + m(t)FV
Choix de fP : La fréquence centrale du signal modulé doit représenter une des fréquences centrales des différentes stations de radiodiffusion MF. Nous avons choisi pour notre simulation une fréquence de l'ordre de fP=5000fs. (En radiodiffusion MF, on a fp~100MHz et fs~15kHz soit fp~6500fs.)
Choix de Fv : ce paramètre détermine l'indice de modulation de notre modulateur. On le choisira de sorte que amFv soit bien supérieur à fk. afin de réaliser une bonne modulation. La bande passante du signal modulé est alors Bs=[fp-amFv , fp+amFv]. (En radiodiffusion MF on a Bs~0.4MHz.)
Nous avons du réaliser un filtre passe-bande numérique, afin de ne conserver en entrée du démodulateur qu'un signal centré en fI , fréquence de démodulation.
Pour cela nous avons utilisé la
fonction Butter pour calculer les vecteurs ![]() et
et ![]() , coefficients d'un filtre de la forme :
, coefficients d'un filtre de la forme : ![]() .
.
Il a alors fallu choisir la fonction Simulink réalisant le filtrage utilisant les vecteurs coefficients de la même manière.
Simulink met à notre disposition
une fonction de démodulation en bande transposée dont les
paramètres sont:
Constante de modulation (en Hz/V) Fv
Feentrée
a4
b4
Fv indique l’indice de modulation. L’amplitude du signal démodulé sera de la forme adem=fp/Fv où fp est la fréquence du signal modulé. Dans un souci d’homogénéité de notre système nous avons gardé la même valeur que celle utilisée pour la modulation.
a4 et b4
sont les vecteurs coefficients d’un filtre numérique
passe-bas dont la fonction de transfert en Z s’écrit :
![]() .
.
Nous avons donc choisi un filtre d’ordre 4 dont la
fréquence de coupure est la bande passante de notre signal avant
modulation.